Geometry formulas are essential for solving problems involving shapes, areas, and volumes. This guide provides a comprehensive collection of formulas for 2D and 3D shapes, including triangles, circles, rectangles, and more. Whether you’re a student or a professional, these resources will help you master geometric calculations and properties.
Overview of Basic Geometric Formulas
Basic geometric formulas provide the foundation for solving problems involving shapes and their properties. For rectangles and squares, the perimeter is calculated as P = 2(l + w) and the area as A = l × w. Circles use the formulas C = 2πr for circumference and A = πr² for area. Triangles have a perimeter of P = a + b + c and an area of A = 1/2 × base × height; These formulas are essential for understanding more complex geometric concepts and are widely used in various fields, from engineering to architecture. Mastering these basics ensures a strong grasp of geometry principles and their applications.
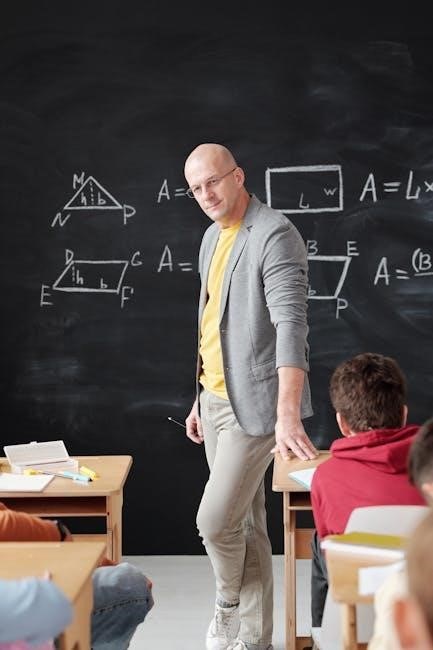
Area and Perimeter Formulas for 2D Shapes
Area and perimeter formulas for 2D shapes are fundamental in geometry. Rectangles and squares use P = 2(l + w) for perimeter and A = l × w for area. Circles utilize C = 2πr for circumference and A = πr² for area. Triangles apply P = a + b + c for perimeter and A = 1/2 × base × height for area. These formulas are essential for calculating dimensions of various 2D shapes, aiding in problem-solving across math and real-world applications.
Rectangle and Square Formulas
Rectangles and squares are fundamental 2D shapes with specific area and perimeter formulas. For a rectangle, the perimeter is calculated as P = 2(l + w), where l is the length and w is the width. The area of a rectangle is A = l × w. A square, being a special type of rectangle with equal sides, has a perimeter of P = 4s or P = 2(2s), where s is the side length. The area of a square is A = s². These formulas are widely used in construction, crafting, and everyday calculations involving rectangular and square shapes.
Circle Formulas

The circle is a fundamental 2D shape with specific geometric formulas. The circumference of a circle is given by C = 2πr, where r is the radius, or C = πd, where d is the diameter. The area of a circle is calculated using A = πr². The diameter is twice the radius, so d = 2r. These formulas are essential for solving problems involving circular shapes, such as calculating distances, areas, and volumes in various fields like engineering, architecture, and design. Understanding these formulas is crucial for mastering geometric calculations and real-world applications involving circular measurements.
Triangle Formulas
Triangles are fundamental shapes in geometry, and their formulas are crucial for solving various problems. The perimeter of a triangle is the sum of its three sides: P = a + b + c. The area can be calculated using the base and height with the formula A = ½ * base * height. For triangles with known side lengths, Heron’s formula is useful: A = √[s(s ─ a)(s ─ b)(s ⎻ c)], where s is the semi-perimeter. In right-angled triangles, the Pythagorean theorem applies: a² + b² = c², where c is the hypotenuse. These formulas are essential for understanding triangle properties and solving problems in fields like construction, physics, and engineering.
Regular Polygon Formulas
Regular polygons have equal sides and angles, making their formulas straightforward. The perimeter of a regular polygon is P = n * s, where n is the number of sides and s is the side length. The area is calculated using the apothem (a), the distance from the center to a side: A = (P * a) / 2. The sum of interior angles is (n ─ 2) * 180°, and each interior angle is [(n ⎻ 2) * 180°] / n. The exterior angle is 360° / n. These formulas are essential for calculating properties like side lengths, apothems, and angles in regular polygons, aiding in both theoretical and practical geometric calculations.

Key Geometry Concepts and Properties
Geometry involves understanding points, lines, angles, and planes. Essential properties include congruence and similarity, while theorems like the Pythagorean theorem and angle sums are fundamental.
Types of Triangles
Triangles are classified based on their sides and angles. A scalene triangle has all sides of different lengths and all angles unequal. An isosceles triangle has two equal sides and two equal angles. An equilateral triangle has all sides and angles equal. Additionally, triangles can be categorized by their angles: acute (all angles less than 90°), right (one 90° angle), and obtuse (one angle greater than 90°). Understanding these types is crucial for applying geometry formulas and solving problems involving area, perimeter, and trigonometric calculations.
Sum of Interior and Exterior Angles
The sum of the interior angles of a polygon is given by the formula (n-2) × 180°, where n is the number of sides. For example, a triangle has an interior angle sum of 180°, while a quadrilateral has 360°. The sum of the exterior angles of any polygon is always 360°, regardless of the number of sides. Each exterior angle is supplementary to its corresponding interior angle, meaning they add up to 180°. These properties are fundamental in solving geometric problems, such as finding unknown angles or verifying the validity of polygon shapes. Understanding these concepts is essential for mastering geometry formulas and their applications.

3D Geometry Formulas
3D geometry involves formulas for calculating surface area and volume of common solids like cubes, spheres, and cylinders. Mastering these formulas is essential for solving complex problems in engineering, architecture, and physics.
Surface Area and Volume of Common Solids
Calculating surface area and volume for 3D shapes is crucial in geometry. For a cube, the surface area is 6s² and volume is s³, where s is the side length. A sphere’s surface area is 4πr² and volume is (4/3)πr³, with r as the radius. For a cylinder, surface area is 2πr(h + r) and volume is πr²h, where r is the radius and h is the height. Understanding these formulas is essential for solving problems in engineering, architecture, and physics.
Pythagorean Theorem and Applications
The Pythagorean Theorem states that in a right-angled triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b), expressed as (a^2 + b^2 = c^2). This fundamental principle has wide-ranging applications in geometry, physics, engineering, and navigation, making it a cornerstone of mathematical problem-solving.
Right Triangle Properties
A right triangle has one 90-degree angle, with the other two angles summing to 90 degrees. The side opposite the right angle is the hypotenuse, the longest side. The Pythagorean Theorem (a² + b² = c²) relates the legs (a, b) and hypotenuse (c). Trigonometric ratios like sine, cosine, and tangent are defined based on the ratios of the sides. Special right triangles, such as 30-60-90 and 45-45-90 triangles, have predictable side ratios, simplifying calculations. These properties are fundamental in geometry, trigonometry, and real-world applications like construction and physics.
Resources for Geometry Formulas
Discover comprehensive PDF guides and online tools offering detailed geometry formulas, examples, and problem-solving tips for various shapes and theorems.
PDF Guides and Online Tools
PDF guides are an excellent resource for accessing geometry formulas in a structured and downloadable format. Many websites offer free PDF downloads that cover essential geometric formulas, including those for 2D and 3D shapes. These guides often include detailed explanations, examples, and diagrams to help users understand and apply the formulas effectively. Online tools, such as formula calculators and interactive geometry software, provide instant calculations and visualizations, making problem-solving more efficient. Platforms like MathJax also enable seamless rendering of mathematical equations in web browsers, enhancing the learning experience. Whether you’re a student or a professional, these resources simplify the process of mastering geometry formulas and their applications.